Wie verhindert man, dass Viren viral werden?

Eigentlich beschäftigte sich der Forscher Markus Sinnl in seiner bisherigen Arbeit mit sozialen Medien wie Twitter. In den vergangenen Jahren entwickelte er Methoden, die klären sollten, wie bestimmte Posts viral werden. Als die Coronapandemie ausbrach, erkannte er, dass die Situation der Ausbreitung von Informationen in sozialen Medien der Ausbreitung des Coronavirus in der Bevölkerung stark ähnelt. In einem vom Wissenschaftsfonds FWF finanzierten Projekt will er nun seine Tools für den Kampf gegen Corona nutzen.

Suche nach exakten Lösungen

Projektleiter Sinnl plant, dazu die für Social Media entwickelten Methoden zu erweitern. Das Virus entspricht hier einem Akteur in einem Netzwerk, der maximale Ausbreitung erreichen will. „Das würden wir genau so modellieren wie die Ausbreitung einer Message in einem sozialen Netzwerk, doch wir wollen noch eine Ebene darüberlegen, mit von außen getroffenen Maßnahmen, die eine Ausbreitung verhindern sollen“, erklärt Sinnl.

Die dabei von Sinnl angewandte Methode nennt sich ganzzahlige Programmierung. Dabei geht es um die Lösungen von Gleichungen, die keine Kommazahlen, sondern nur ganze Zahlen enthalten. Viele praktische Probleme in der Industrie oder beispielsweise bei Fahrplänen im öffentlichen Verkehr lassen sich auf diese Weise gut behandeln. Darauf weist auch Sinnls Arbeitsumfeld am Institut für Produktions- und Logistikmanagement der Johannes Kepler Universität Linz hin. Der Vorteil der ganzzahligen Programmierung: Die Gleichungen liefern mehr als nur Wahrscheinlichkeiten. „Unsere Methoden geben die beweisbar optimale Lösung des Problems an“, betont Sinnl.

Methoden aus Werbung

„In den letzten Jahren habe ich ganzzahlige Programmierung unter anderem zum Lösen von Influence-Maximisation angewandt“, erzählt er. „Die Frage war: Wie kann man in sozialen Netzwerken Leute beeinflussen?“ Solche Probleme hätten durchaus eine Tradition in den Computerwissenschaften, so der Forscher, doch die meisten versuchten, sie „heuristisch“ zu lösen, also Näherungslösungen zu finden.

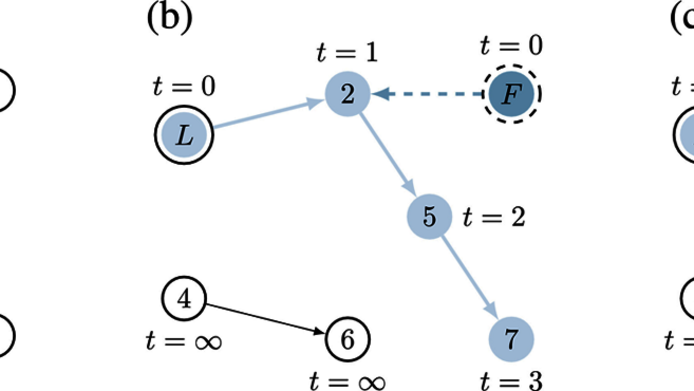
In der Beschreibung der Ausbreitungsdynamik des Coronavirus seien exakte Lösungen eine Neuerung, auch dort wird bisher mit heuristischen Methoden und Näherungslösungen gearbeitet. Außerdem würden bestimmte Maßnahmen zur Verhinderung der Ausbreitung zwar mit Modellen auf ihre Wirksamkeit geprüft, erklärt der Forscher, doch ob das auch die optimale Lösung ist, lasse sich kaum feststellen. Sinnl hingegen nähert sich der Situation, indem er sie als Optimierungsproblem betrachtet. Er bildet verschiedene Maßnahmen zur Reduktion der Ausbreitung in seinen Methoden ab und sucht dann direkt die optimale Kombination.