Statistics for snow forecasting

In recent decades, the quality of weather forecasts has greatly improved thanks to the development of increasingly powerful computer methods. Forecast periods have become longer and the predictions more accurate. But where there are complex local conditions even the most up-to-date weather models reach their limits. There is usually just one single forecast for areas covering hundreds of square kilometres, which results in considerable inaccuracies in mountainous regions. The consequences are manifold, especially where expected quantities of snow are concerned, a topic of great importance for tourism. Safety is of particular relevance in this regard. In a project funded by the Austrian Science Fund FWF, an Innsbruck-based research group combining experts from meteorology and statistics has now compared data from conventional weather models with local measurements from the past in order to derive more precise local forecasts, especially for snowfall.
Taking historical weather observations into account
“In global numerical weather simulations, as used for weather reports, the grid size of the models is relatively large, usually 20 x 20 km, sometimes 50 x 50 km”, explains the principal investigator Achim Zeileis. “But if you look out the window in Tyrol, you will see with your own eyes that the weather can vary several times over a distance of 20 kilometres, one of the reasons being the mountain ridges that are not captured by the numerical model.” According to Zeileis, it is virtually impossible to create an exact physical model of such complex local features. On the other hand, there are many local weather stations that can provide more detailed information about what the weather was like in the past. These could be used for local corrections of conventional weather forecasts.
“We collect and combine weather data from the past to understand how the weather really turned out when numerical weather simulations generated a given prediction”, Zeileis explains. “Did the weather tend to be warmer or colder, was there more or less rain than forecast?” Researchers use the term “standardised anomalies” in this context. - They try to statistically record deviations that recur frequently and use this as a basis to adjust the predictions for a given local context. “These forecasts are, of course, still not accurate, sometimes considerably so, but they are often much better than what conventional weather models come up with”, notes Zeileis in the interview with scilog.
Merging different data
The processing of the measurement data was very complicated for predicting snow, explains Reto Stauffer, a member of the project team who completed his doctorate in the course of the research project. For forecasting snow, one needs information about both temperature and precipitation. “We had access to many different data sources. For the forecast of snow quantities it was particularly important to have long time scales, because precipitation is extremely variable. A year or two won't do.” The team focused on obtaining temperature measurements and precipitation measurements from two different networks. The latter came from the Hydrographic Service, because their data go back forty or fifty years, while the former came from the national weather service, which has a large number of stations. “For the temperature it was enough to have data for the last ten or fifteen years.” Various products of the European Centre for Medium-Range Weather Forecasts (ECMWF) were used for the numerical weather model, including a product that is actually designed for climatology and allows precise estimates of precipitation. For the project research it was not necessary to know more about the physical processes at the respective location. Although the team did try to include physical variables, for example slope alignment, this did not help them much for forecasting.
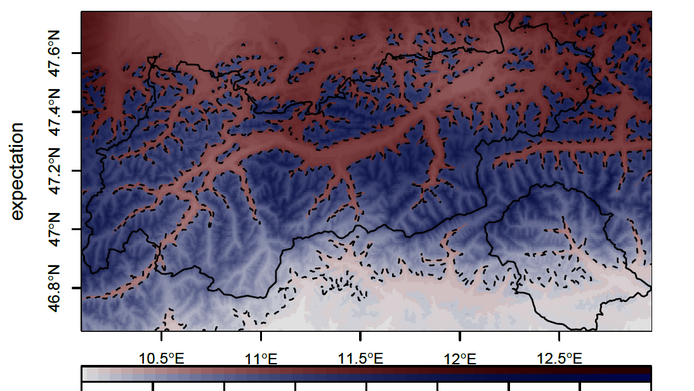
Focus on Tyrol
For their computation of expected snowfall, the researchers concentrated on Tyrol. Zeileis stresses that this type of research is particularly interesting for mountain regions: “In lowland areas there are no such major errors in the global weather simulations, because the terrain does not vary as much.” For other projects they also looked inter alia at South Tyrol. Achim Zeileis emphasises that this is basic research, although the issue at hand is of great societal interest. The statistical model developed by his group, which uses the above-mentioned standardised anomalies, is already being deployed in some places. The prediction methods for snow quantities have only recently been published. “We have a flexible tool here that may be relevant for various practical applications in the future”, says Zeileis.
Personal details
Achim Zeileis is a professor at the Department of Statistics at the University of Innsbruck. The statistician is particularly interested in weather forecasting, statistical modelling, statistical software and machine learning.
Publications
Reto Stauffer, Georg J. Mayr, Jakob W. Messner, Achim Zeileis: Hourly Probabilistic Snow Forecasts over Complex Terrain: A Hybrid Ensemble Postprocessing Approach. Advances in Statistical Climatology, Meteorology and Oceanography, accepted for publication, 2018
Markus Dabernig, Georg J. Mayr, Jakob W. Messner, Achim Zeileis: Spatial Ensemble Post-Processing with Standardized Anomalies. Quarterly Journal of the Royal Meteorological Society, 2017
Reto Stauffer, Nikolaus Umlauf, Jakob W. Messner, Georg J. Mayr, Achim Zeileis: Ensemble Post-Processing of Daily Precipitation Sums over Complex Terrain Using Censored High-Resolution Standardized Anomalies. Monthly Weather Review, 2017
Jakob W. Messner, Georg J. Mayr, Achim Zeileis: Heteroscedastic Censored and Truncated Regression with crch. The R Journal, 2016 (pdf)